재귀함수(recursion)!
🦥 재귀함수
- 정의 단계에서 자신을 재참조하는 함수
- 전달되는 상태인 매개변수가 달라질뿐 똑같은 일을 하는 함수
- 큰 문제를 작은 부분문제로 나눠서 풀 때 사용한다.
주의사항
- 반드시 기저사례를 써야한다. (종료조건, 무한히 반복 안되게)
- 사이클이 있다면 쓰면 안된다. ex) f(a) 가 f(b)를 호출한 뒤 f(b)가 다시 f(a)를 호출하는 것.
- 반복문으로 될거 같으면 반복문으로. (함수호출에 대한 코스트)
예시
- 팩토리얼 n! : 그 이전의 항을 모두 곱하는 것. 곱한다는 행위의 반복! 3! -> 3x2x1 = 6
- 피보나치 : 수학에서, 피보나치 수는 첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열이다. 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144
팩토리얼
a! = (a-1)(a-2)(a-n)…
코드
int fact(int n) {
if(n == 1 || n == 0) return 1;
return n * fact(n-1);
}
그런데 팩토리얼 같은 경우는 반복문으로 작성이 가능하다. 그러니 재귀함수보단 반복문이 가능하면 작성해주자! 왜냐, 재귀함수는 오래걸리고 너무 많이 자기를 호출하기 때문이다.
int loop(int n) {
int result = 1;
for(int i = 1; i <= n; i ++) {
result *= i;
}
return result;
}
피보나치 수열
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144
f(6) = f(5) + f(4) -> 8 f(5) = f(4) + f(3) -> 5 f(4) = f(3) + f(2) -> 3 f(3) = f(2) + f(1) -> 2 f(2) = f(1) + f(0) -> 1 f(1) -> 1 f(0) -> 0
코드
int fibo(int n) {
if(n == 0 || n == 1) return n;
return fibo(n-1) + fibo(n-2);
}
## C++ 로 코드 정리
#include <bits/stdc++.h>
using namespace std;
int fact(int n) {
if (n == 1 || n == 0) return 1;
return n * fact(n - 1);
}
// 팩토리얼 반복문으로 작성
int loop(int n) {
int result = 1;
for (int i = 1; i <= n; i++) {
result *= i;
}
return result;
}
// 피보나치 수열
int fibo(int n) {
if (n == 0 || n == 1) return n;
return fibo(n - 1) + fibo(n - 2);
}
// n 은 초기값 4로 선언
int n = 4;
int main() {
// 출력
cout << "팩토리얼 결과 : " << fact(n) << ", 피보나치수열 결과 : " << fibo(n) << "\n";
return 0;
}
/*
결과
팩토리얼 결과 : 24, 피보나치수열 결과 : 3
*/
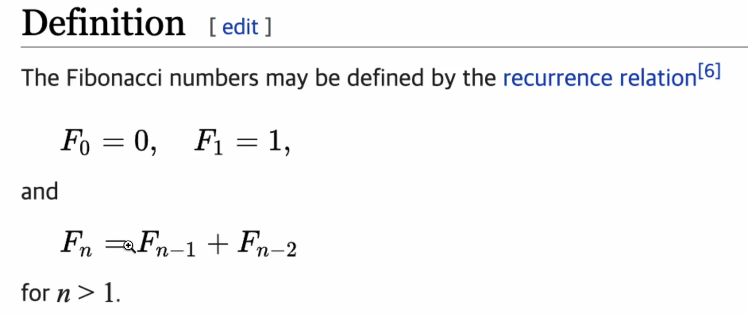
Leave a comment